A really powerful tool in Computer Aided Design (CAD) is the ability to apply “constraints” to your drawing. Constraints are a really powerful tool, allowing the drafter to declare how parts of their drawing are related, then letting the CAD program figure out how parameters can be manipulated in such a way that
You can think of a constraint as some sort of mathematical relationship between two or more parameters.
Some examples are:
- “This interior angle is 45°”
- “That line is vertical”
- “Side A is perpendicular to side B”
Graphically they’ll be displayed something like this:
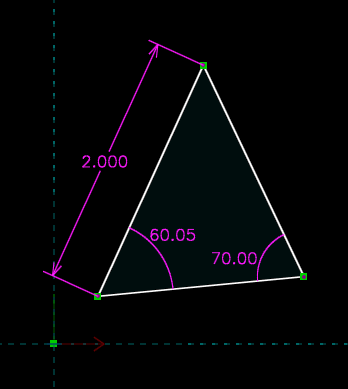
A constrained triangle in SolveSpace
These constraints are declared mathematically, so a “This line is vertical” constraint may be written as $line.start.x - line.end.x = 0$ and $line.start.z - line.end.z = 0$ (assuming the $x$ axis is to the right and the $z$ comes out of the page).
In response to input from the user (e.g. they click on the line and drag it to the left), a constraint system will feed the perturbation into the system of equations (e.g. the $line.start.y$ changes by $-0.1$ units) and based on the available constraints and tie-breaking heuristics, it will figure out how much each remaining variable must change. Execute at 60 FPS and you’ve got an interactive, parametric CAD application.
A constraint solver is a fairly complex system, but the first step is teaching it how to manipulate and evaluate abstract maths.
The code written in this article is available on GitHub. Feel free to browse through and steal code or inspiration.
If you found this useful or spotted a bug, let me know on the blog’s issue tracker!
The Expression Tree Link to heading
For this constraint solver we need a way to represent algebraic expressions like $x - 5$ or $sin(x) + y*y - x*y$, and the most natural form is the Abstract Syntax Tree.
In this language, an expression can be:
- A (possibly unnamed) parameter
- A floating-point constant
- A call to a function with a single argument
- Negation, and
- A binary operation (e.g.
x + y, wherexandyare theleftandrightoperands, and we’re using the+operator)
Our constraint solver is considerably less complex than a general purpose programming language, so most of our Abstract Syntax Tree can fit into a couple simple types.
// src/expr.rs
use std::rc::Rc;
use smol_str::SmolStr;
/// An expression.
#[derive(Debug, Clone, PartialEq)]
pub enum Expression {
/// A free variable (e.g. `x`).
Parameter(Parameter),
/// A fixed constant (e.g. `3.14`).
Constant(f64),
/// An expression involving two operands.
Binary {
/// The left operand.
left: Rc<Expression>,
/// The right operand.
right: Rc<Expression>,
/// The binary operation being executed.
op: BinaryOperation,
},
/// Negate the expression.
Negate(Rc<Expression>),
/// Invoke a builtin function.
FunctionCall {
/// The name of the function being called.
name: SmolStr,
/// The argument passed to this function call.
argument: Rc<Expression>,
},
}
/// A free variable.
#[derive(Debug, Clone, PartialEq, PartialOrd, Ord, Eq, Hash)]
pub enum Parameter {
/// A variable with associated name.
Named(SmolStr),
/// An anonymous variable generated by the system.
Anonymous { number: usize },
}
/// An operation that can be applied to two arguments.
#[derive(Debug, Copy, Clone, PartialEq)]
pub enum BinaryOperation {
Plus,
Minus,
Times,
Divide,
}
This should be fairly straightforward if you are familiar with Rust, although I’d like to direct your attention to two details…
- Text fields use a
smol_str::SmolStrinstead of a normalString - Each child node is behind a reference-counted pointer
We’re using SmolStr for something called the Small String Optimisation.
This is where small amounts of text can be stored inline on the stack (in place
of the data pointer, length, and capacity fields in a normal String) to skip
a heap allocation and a layer of indirection.
The small string optimisation is useful when you’re dealing with a large
number of small strings (like programming language identifiers) because it
helps avoid heap fragmentation and locality. Cloning a SmolStr is also
quite cheap because even if it isn’t small, a reference-counted string
(analogous to Arc<str>) is used when we need to store large strings on the
heap.
A conscious design decision is to make the AST immutable. Most operations
applied to an Expression will leave part of the tree unchanged, and seeing
as we already need to add a layer of indirection to prevent infinitely
sized types, we can use reference-counted pointers to share
common sub-expressions.
This should reduce memory usage and hopefully increase performance because shared nodes are more likely to be in cache.
Pretty-Printing and Other Useful Methods Link to heading
To make our Expression type easier to work with we can implement several
traits from the standard library.
Arguably the most useful of these is std::fmt::Display, a mechanism for
getting the Expression’s human-readable form.
Writing the Display Implementation Link to heading
To help make writing parentheses and spaces in Display a bit easier, let’s
create a temporary type for handling operator precedence.
// src/expr.rs
#[derive(Debug, Copy, Clone, PartialEq, PartialOrd)]
enum Precedence {
Bi,
Md,
As,
}
The mnemonic I learned in school was BIMDAS, short for Brackets, Indices, Multiply and Divide, and Addition and Subtraction. Hence the cryptic variant names.
We don’t support exponents (yet?), so it’s fine for Brackets and Indices to be in the same precedence variant.
We also define some helper methods for getting an Expression’s precedence.
In this case parameters, constants, and function calls all have the highest
possible precedence level.
// src/expr.rs
impl Expression {
fn precedence(&self) -> Precedence {
match self {
Expression::Parameter(_)
| Expression::Constant(_)
| Expression::FunctionCall { .. } => Precedence::Bi,
Expression::Negate(_) => Precedence::Md,
Expression::Binary { op, .. } => op.precedence(),
}
}
}
impl BinaryOperation {
fn precedence(self) -> Precedence {
match self {
BinaryOperation::Plus | BinaryOperation::Minus => Precedence::As,
BinaryOperation::Times | BinaryOperation::Divide => Precedence::Md,
}
}
}
Printing a Parameter works by either printing the name as-is, or the
parameter number preceded by a $ if it is anonymous (i.e. $2).
// src/expr.rs
use std::fmt::{self, Display, Formatter};
impl Display for Parameter {
fn fmt(&self, f: &mut Formatter<'_>) -> fmt::Result {
match self {
Parameter::Named(name) => write!(f, "{}", name),
Parameter::Anonymous { number } => write!(f, "${}", number),
}
}
}
In Expression’s Display implementation we just need to do a match and
use the write!() macro to generate the desired string for each variant.
// src/expr.rs
impl Display for Expression {
fn fmt(&self, f: &mut Formatter<'_>) -> fmt::Result {
match self {
Expression::Parameter(p) => write!(f, "{}", p),
Expression::Constant(value) => write!(f, "{}", value),
Expression::Binary { left, right, op } => {
write_with_precedence(op.precedence(), left, f)?;
let middle = match op {
BinaryOperation::Plus => " + ",
BinaryOperation::Minus => " - ",
BinaryOperation::Times => "*",
BinaryOperation::Divide => "/",
};
write!(f, "{}", middle)?;
write_with_precedence(op.precedence(), right, f)?;
Ok(())
},
Expression::Negate(inner) => {
write!(f, "-")?;
write_with_precedence(
BinaryOperation::Times.precedence(),
inner,
f,
)?;
Ok(())
},
Expression::FunctionCall { name, argument } => {
write!(f, "{}({})", name, argument)
},
}
}
}
fn write_with_precedence(
current_precedence: Precedence,
expr: &Expression,
f: &mut Formatter<'_>,
) -> fmt::Result {
if expr.precedence() > current_precedence {
// we need parentheses to maintain ordering
write!(f, "({})", expr)
} else {
write!(f, "{}", expr)
}
}
The write_with_precedence() helper is used to make sure our pretty-printer
respects the precedence of its operands by adding parentheses when necessary.
This prevents awkward bugs like -(x + 3) being printed as -x + 3.
We also deliberately add space before and after operators with the
Precedence::As precedence to help visually separate the different terms in an
expression.
The Display implementation is really easy to test. Just create a list of
tuples containing an Expression and its expected string representation,
then loop over asserting each gets formatted as desired.
Long table-based pretty-printer test
// src/expr.rs
#[test]
fn pretty_printing_works_similarly_to_a_human() {
let inputs = vec![
(Expression::Constant(3.0), "3"),
(
Expression::FunctionCall {
name: "sin".into(),
argument: Rc::new(Expression::Constant(5.0)),
},
"sin(5)",
),
(
Expression::Negate(Rc::new(Expression::Constant(5.0))),
"-5",
),
(
Expression::Negate(Rc::new(Expression::FunctionCall {
name: "sin".into(),
argument: Rc::new(Expression::Constant(5.0)),
})),
"-sin(5)",
),
(
Expression::Binary {
left: Rc::new(Expression::Constant(1.0)),
right: Rc::new(Expression::Constant(1.0)),
op: BinaryOperation::Plus,
},
"1 + 1",
),
(
Expression::Binary {
left: Rc::new(Expression::Constant(1.0)),
right: Rc::new(Expression::Constant(1.0)),
op: BinaryOperation::Minus,
},
"1 - 1",
),
(
Expression::Binary {
left: Rc::new(Expression::Constant(1.0)),
right: Rc::new(Expression::Constant(1.0)),
op: BinaryOperation::Times,
},
"1*1",
),
(
Expression::Binary {
left: Rc::new(Expression::Constant(1.0)),
right: Rc::new(Expression::Constant(1.0)),
op: BinaryOperation::Divide,
},
"1/1",
),
(
Expression::Negate(Rc::new(Expression::Binary {
left: Rc::new(Expression::Constant(1.0)),
right: Rc::new(Expression::Constant(1.0)),
op: BinaryOperation::Plus,
})),
"-(1 + 1)",
),
(
Expression::Negate(Rc::new(Expression::Binary {
left: Rc::new(Expression::Constant(1.0)),
right: Rc::new(Expression::Constant(1.0)),
op: BinaryOperation::Times,
})),
"-1*1",
),
(
Expression::Binary {
left: Rc::new(Expression::Binary {
left: Rc::new(Expression::Constant(1.0)),
right: Rc::new(Expression::Constant(2.0)),
op: BinaryOperation::Plus,
}),
right: Rc::new(Expression::Constant(3.0)),
op: BinaryOperation::Divide,
},
"(1 + 2)/3",
),
(
Expression::Binary {
left: Rc::new(Expression::Constant(3.0)),
right: Rc::new(Expression::Binary {
left: Rc::new(Expression::Constant(1.0)),
right: Rc::new(Expression::Constant(2.0)),
op: BinaryOperation::Times,
}),
op: BinaryOperation::Minus,
},
"3 - 1*2",
),
];
for (expr, should_be) in inputs {
let got = expr.to_string();
assert_eq!(got, should_be);
}
}
Operator Overloads Link to heading
The use of operator overloads can often be quite controversial, but in this
case I think it could help add some level of syntactic sugar to
make constructing Expressions more readable.
In this case, we’ll overload the normal binary operators so they wrap the left
and right operands with an Expression::Binary.
// src/expr.rs
use std::ops::{Add, Div, Mul, Sub};
// define some operator overloads to make constructing an expression easier.
impl Add for Expression {
type Output = Expression;
fn add(self, rhs: Expression) -> Expression {
Expression::Binary {
left: Rc::new(self),
right: Rc::new(rhs),
op: BinaryOperation::Plus,
}
}
}
impl Sub for Expression {
type Output = Expression;
fn sub(self, rhs: Expression) -> Expression {
Expression::Binary {
left: Rc::new(self),
right: Rc::new(rhs),
op: BinaryOperation::Minus,
}
}
}
impl Mul for Expression {
type Output = Expression;
fn mul(self, rhs: Expression) -> Expression {
Expression::Binary {
left: Rc::new(self),
right: Rc::new(rhs),
op: BinaryOperation::Times,
}
}
}
impl Div for Expression {
type Output = Expression;
fn div(self, rhs: Expression) -> Expression {
Expression::Binary {
left: Rc::new(self),
right: Rc::new(rhs),
op: BinaryOperation::Divide,
}
}
}
While we’re at it, let’s add a Neg impl so you can write things like -x.
// src/expr.rs
use std::ops::Neg;
impl Neg for Expression {
type Output = Expression;
fn neg(self) -> Self::Output { Expression::Negate(Rc::new(self)) }
}
You can see none of these operator overloads are particularly interesting, they just let us avoid a bunch of typing.
Iterators Link to heading
A useful building block for working with the Expression tree is being able
to iterate over every node in the tree. Imagine scanning through a big
expression to figure out which parameters it references or the functions that
it calls.
To do this, we’ll create an iter() method which returns something
implementing Iterator<Item = &Expression>.
// src/expr.rs
impl Expression {
/// Iterate over all [`Expression`]s in this [`Expression`] tree.
pub fn iter(&self) -> impl Iterator<Item = &Expression> + '_ {
Iter {
to_visit: vec![self],
}
}
}
/// A depth-first iterator over the sub-[`Expression`]s in an [`Expression`].
#[derive(Debug)]
struct Iter<'expr> {
to_visit: Vec<&'expr Expression>,
}
The Iter type works by maintaining a list of &Expression references for the
nodes it still needs to visit. Getting the next_item is then just a case of
popping a reference from the list, queueing any sub-expressions under
next_item itself before returning it.
// src/expr.rs
impl<'expr> Iterator for Iter<'expr> {
type Item = &'expr Expression;
fn next(&mut self) -> Option<Self::Item> {
let next_item = self.to_visit.pop()?;
match next_item {
Expression::Binary { left, right, .. } => {
self.to_visit.push(right);
self.to_visit.push(left);
},
Expression::Negate(inner) => self.to_visit.push(inner),
Expression::FunctionCall { argument, .. } => {
self.to_visit.push(argument)
},
_ => {},
}
Some(next_item)
}
}
This enables nice things like an iterator over all referenced parameters or functions, and checking whether an expression depends on a parameter.
// src/expr.rs
impl Expression {
/// Iterate over all [`Parameter`]s mentioned in this [`Expression`].
pub fn params(&self) -> impl Iterator<Item = &Parameter> + '_ {
self.iter().filter_map(|expr| match expr {
Expression::Parameter(p) => Some(p),
_ => None,
})
}
/// Does this [`Expression`] involve a particular [`Parameter`]?
pub fn depends_on(&self, param: &Parameter) -> bool {
self.params().any(|p| p == param)
}
/// Iterate over all functions used by this [`Expression`].
pub fn functions(&self) -> impl Iterator<Item = &str> + '_ {
self.iter().filter_map(|expr| match expr {
Expression::FunctionCall { name, .. } => Some(name.as_ref()),
_ => None,
})
}
}
Parsing Link to heading
Now you may be wondering why we’d mention parsing in an article about
creating a geometric constraints system, and the answer is quite simple…
Constructing a full Expression tree using object literals is really verbose
and annoying. In turn, this increases the effort required to write and maintain
tests,
It’s also useful if we want to provide users with a text box so they can
enter their own custom constraints. SolidWorks uses this to let an engineer
specify entire families of designs who’s final dimensions are driven by one
or two parameters (this is often referred to as a
“Configuration”). For example, imagine having a proprietary
*bolt design and being able to say “I want this as an M6x1.0” (initial
parameters are outside_diameter = 6.0 millimetres, thread_pitch = 1.0
threads per millimetre) and the constraints system figuring out all the other
dimensions.
Besides letting the end user or developer input enter an expression into the
computer in textual form, it can also be a powerful tool during development.
In combination with our earlier pretty-printer, you can use strings to
concisely say what an Expression should look like before and after a
particular operation.
Throw in a macro or two and a suite of unit tests for testing various expression operations could look like this:
expr_test!(simplify_multiplication, "2*2 + x" => fold_constants => "4 + x");
expr_test!(simplify_sine_90_degrees, "sin(90)" => fold_constants => "1");
expr_test!(differentiate_cos, "cos(t)" => partial_derivative(t) => "-sin(t)");
expr_test!(evaluate_tricky_expression, "10 - 2*x + x*x" => evaluate(x: 5.0) => "25");
The process of turning unstructured text into a more structured form, an
Expression tree in our case, is commonly referred to as “parsing”.
While you could hack something together using string operations or even a regular expression or two, this approach will often fall over the moment you give it more complex expressions (e.g. using parentheses to nest expressions inside expressions) or if different levels of precedence are involved.
If you are initially tempted to parse a non-trivial expression using regular expressions, I would invite you to first read this famous StackOverflow answer.
The underlying problem is that an expression is something called a Context Free Language, while a regular expression is based on a Regular Language. To parse a Regular Language you (in theory) just need to keep track of the current state (a state machine), however Context Free Languages require you to track not just the current state, but also support nesting and keep track of each nested state (a pushdown automata).
Google the Chomsky Hierarchy for more.
Tokenising Link to heading
Often the first step in turning an unstructured string of characters into a
structured Expression tree is Tokenisation. This is where the
string is broken up into the “atoms” of our language (aka Tokens), so
things like identifiers ("foo"), numbers ("3.14"), punctuation ("("),
and operators ("+").
We also keep track of where each Token occurred in the source text. That
way we’ve got somewhere to point to when reporting errors to the user.
By pre-processing a stream of text into a slightly more high-level representation your parser can operate at the granularity of tokens (e.g. a number, plus symbol, or an identifier) instead of needing to process individual characters.
// src/parse.rs
use std::ops::Range;
#[derive(Debug, Clone, PartialEq)]
struct Token<'a> {
text: &'a str,
span: Range<usize>,
kind: TokenKind,
}
/// The kinds of token that can appear in an [`Expression`]'s text form.
#[derive(Debug, Copy, Clone, PartialEq)]
pub enum TokenKind {
Identifier,
Number,
OpenParen,
CloseParen,
Plus,
Minus,
Times,
Divide,
}
We use the Iterator trait to represent a stream of tokens. For our
purposes, a Tokens stream wraps a &str and uses a cursor variable to
keep track of where it has read up to. I’ve attached a couple helper methods
for seeing what text is remaining.
// src/parse.rs
#[derive(Debug, Clone, PartialEq)]
struct Tokens<'a> {
src: &'a str,
cursor: usize,
}
impl<'a> Tokens<'a> {
fn new(src: &'a str) -> Self { Tokens { src, cursor: 0 } }
fn rest(&self) -> &'a str { &self.src[self.cursor..] }
fn peek(&self) -> Option<char> { self.rest().chars().next() }
}
While it’s nice to see what text is remaining, we also need a way to advance
the cursor along the string.
// src/parse.rs
impl<'a> Tokens<'a> {
fn advance(&mut self) -> Option<char> {
let c = self.peek()?;
self.cursor += c.len_utf8();
Some(c)
}
}
If you wanted to, you could implement the rest of the Tokens type purely using
calls to peek() and advance(), but sometimes it’s easier to have a more
high-level primitive.
For this sort of thing I’ll typically use some sort of take_while() method
which accepts a predicate and will keep advancing the cursor until the
predicate doesn’t like the next character in line.
// src/parse.rs
impl<'a> Tokens<'a> {
fn take_while<P>(
&mut self,
mut predicate: P,
) -> Option<(&'a str, Range<usize>)>
where
P: FnMut(char) -> bool,
{
let start = self.cursor;
while let Some(c) = self.peek() {
if !predicate(c) { break; }
self.advance();
}
let end = self.cursor;
if start != end {
let text = &self.src[start..end];
Some((text, start..end))
} else {
None
}
}
}
By stashing away the cursor’s value before and after looping we can
calculate the range of characters that have been consumed, and whether
anything was consumed at all.
Reading a token from the stream is just a case of peeking at the next
character, and executing a match statement based on what we find. Something
to keep in mind is we don’t care about whitespace, so the entire thing is
executed in a loop which will keep skipping whitespace until we encounter
something else.
// src/parse.rs
impl<'a> Iterator for Tokens<'a> {
type Item = Result<Token<'a>, ParseError>;
fn next(&mut self) -> Option<Self::Item> {
loop {
return match self.peek()? {
space if space.is_whitespace() => {
self.advance();
continue;
},
'(' => self.chomp(TokenKind::OpenParen),
')' => self.chomp(TokenKind::CloseParen),
'+' => self.chomp(TokenKind::Plus),
'-' => self.chomp(TokenKind::Minus),
'*' => self.chomp(TokenKind::Times),
'/' => self.chomp(TokenKind::Divide),
'_' | 'a'..='z' | 'A'..='Z' => {
Some(Ok(self.chomp_identifier()))
},
'0'..='9' => Some(Ok(self.chomp_number())),
other => Some(Err(ParseError::InvalidCharacter {
character: other,
index: self.cursor,
})),
};
}
}
}
The next() method makes use of several helper methods, the simplest of
which is chomp() for reading a single character as a Token with the
specified TokenKind.
// src/parse.rs
impl<'a> Tokens<'a> {
fn chomp(
&mut self,
kind: TokenKind,
) -> Option<Result<Token<'a>, ParseError>> {
let start = self.cursor;
self.advance()?;
let end = self.cursor;
let tok = Token {
text: &self.src[start..end],
span: start..end,
kind,
};
Some(Ok(tok))
}
We’re also introducing chomp_identifier() for consuming an entire
identifier (i.e. anything that would match the regex, [\w_][\w\d_]*), and
chomp_number() for extracting a floating-point number (which I’m just
defining as the regex \d+(\.\d*)?, because I’m too lazy to worry about the
1e-5 notation for now).
It’s overkill to actually pull in the regex crate for simple patterns like
these though, so we leverage our existing take_while() function and the
fact that closures can use variables from an outside scope to change their
behaviour.
First, let’s look at how chomp_number() is implemented.
// src/parse.rs
impl<'a> Tokens<'a> {
fn chomp_number(&mut self) -> Token<'a> {
let mut seen_decimal_point = false;
let (text, span) = self
.take_while(|c| match c {
'.' if !seen_decimal_point => {
seen_decimal_point = true;
true
},
'0'..='9' => true,
_ => false,
})
.expect("We know there is at least one digit in the input");
Token {
text,
span,
kind: TokenKind::Number,
}
}
}
The idea is we want to keep consuming digits, but only accept the first .
character we see (hence the seen_decimal_point flag). That allows us to
recognise input like 1234, 12.34, and .1234 as numbers, but reject
things like 1.2.3.4 or 1..23.
We do something very similar in chomp_identifier(), where we want to make
sure the first character is either a letter or _, but all characters after
that can be also contain digits.
// src/parse.rs
impl<'a> Tokens<'a> {
fn chomp_identifier(&mut self) -> Token<'a> {
let mut seen_first_character = false;
let (text, span) = self
.take_while(|c| {
if seen_first_character {
c.is_alphabetic() || c.is_ascii_digit() || c == '_'
} else {
seen_first_character = true;
c.is_alphabetic() || c == '_'
}
})
.expect("We know there should be at least 1 character");
Token {
text,
span,
kind: TokenKind::Identifier,
}
}
}
Parsing Using Recursive Descent Link to heading
Arguably one of the most intuitive ways to parse text is a technique called Recursive Descent. This is a top-down method that uses recursive functions to turn a stream of tokens into a tree.
I like using recursive descent because once you’ve figured out your grammar (a file is zero or more statements, a statement maybe an assignment or if-statement, etc.) turning that into code just becomes a case of writing one function per rule and matching different things depending on what the rule asks for.
I’ll often create a Parser type which wraps a Tokens stream. You don’t
need to do it this way, but I like how I can put the grammar in the
*Parser’s doc-comment so if I need to revisit the code 6 months for now I
can pull up the API docs and immediately get a feel for how an Expression
is parsed.
// src/parse.rs
use std::iter::Peekable;
/// A simple recursive descent parser (`LL(1)`) for converting a string into an
/// expression tree.
///
/// The grammar:
///
/// ```text
/// expression := term "+" expression
/// | term "-" expression
/// | term
///
/// term := factor "*" term
/// | factor "/" term
/// | factor
///
/// factor := "-" term
/// | IDENTIFIER "(" expression ")"
/// | IDENTIFIER
/// | "(" expression ")"
/// | NUMBER
/// ```
#[derive(Debug, Clone)]
pub(crate) struct Parser<'a> {
tokens: Peekable<Tokens<'a>>,
}
You may notice that we’ve wrapped our Tokens in a std::iter::Peekable.
This lets us peek at the next token when we need more information about how
to proceed. For example, when processing the expression rule from above, we
after parse one term we can peek at the next token to see if it is a + or
-.
An alternative to looking ahead is to try something anyway and backtrack if it doesn’t work. This might let us simplify the code a bit, but comes with the disadvantage that parsing time can become exponential in the face of poor (or maliciously crafted) input.
Using a lookahead of one token lets us make performance much more consistent.
Rust’s regex crate avoids arbitrary lookahead and back-references for similar
reasons.
To help provide better error messages than just “this expression is invalid”,
we’ve defined a ParseError type representing the various errors that may
occur.
For example, we could encounter an InvalidCharacter while tokenising or run
out of tokens when we are expecting more (e.g. 42 + would result in a
ParseError::UnexpectedEndOfInput), or we could run into a token that isn’t
valid in that context (imagine seeing a + when we’re expecting a number or
identifier).
// src/parse.rs
/// Possible errors that may occur while parsing.
#[derive(Debug, Clone, PartialEq)]
pub enum ParseError {
InvalidCharacter {
character: char,
index: usize,
},
UnexpectedEndOfInput,
UnexpectedToken {
found: TokenKind,
span: Range<usize>,
expected: &'static [TokenKind],
},
}
The key to writing a Recursive Descent parser is to write down the rules so
you know what to expect. For example, lets look at the top-level expression
rule.
expression := term "+" expression
| term "-" expression
| term
Order is important here.
When specifying the expression rule, I’ve taken care to put the more
specific term, term, towards the left and then recurse on the right.
Matching on the more specific thing first takes you closer to the base case
and prevents infinite recursion (I need to parse an expression in order to
parse an expression in order to parse an expression …).
Now, to parse an expression we need to first parse a term (which we’ll
define shortly) then look ahead to check whether it is followed by a + or
- so we know whether we need to parse the right side.
// src/parse.rs
impl<'a> Parser<'a> {
fn expression(&mut self) -> Result<Expression, ParseError> {
let left = self.term()?;
match self.peek() {
// term + expression
Some(TokenKind::Add) => {
let _plus_sign = self.advance();
let right = self.expression()?;
Ok(left + right)
},
// term - expression
Some(TokenKind::Sub) => {
let _minus_sign = self.advance();
let right = self.expression()?;
Ok(left - right)
},
// term
_ => Ok(left)
}
}
fn term(&mut self) -> Result<Expression, ParseError> {
todo!()
}
/// What kind of token is the next one in our `Tokens` stream?
fn peek(&mut self) -> Option<TokenKind> { ... }
/// Advance the `Tokens` stream by one, returning the token that was
/// consumed.
fn advance(&mut self) -> Option<Token> { ... }
}
You can see how this code almost exactly reflects the expression. You’ll
see that there’s a lot you can do to remove code duplication, but for our
purposes it’s not necessary.
I chose to reuse our operator overloads, though. They make constructing binary expressions slightly less verbose.
Next comes the term rule.
term := factor "*" term
| factor "/" term
| factor
You can see that the term rule is almost identical, except it looks for *
and /.
There’s no point copy-pasting the expression() method here, so let’s jump
straight into factor.
factor := "-" factor
| IDENTIFIER "(" expression ")"
| IDENTIFIER
| "(" expression ")"
| NUMBER
Finally we reach something interesting.
This rule matches a bunch of things which all have the same precedence level:
- Negated
factors (i.e.-(x + y)) - Function calls
- Variables
- Nested
expressions inside parentheses, or - Number
The code is fairly similar to before, except we’ve got a larger match
statement.
// src/parse.rs
impl<'a> Parser<'a> {
fn factor(&mut self) -> Result<Expression, ParseError> {
match self.peek() {
// NUMBER
Some(TokenKind::Number) => {
return self.number();
},
// "-" factor
Some(TokenKind::Minus) => {
let _ = self.advance()?;
let operand = self.factor()?;
return Ok(-operand);
},
// IDENTIFIER | IDENTIFIER "(" expression ")"
Some(TokenKind::Identifier) => {
return self.variable_or_function_call()
},
// "(" expression ")"
Some(TokenKind::OpenParen) => {
let _ = self.advance()?;
let expr = self.expression()?;
let close_paren = self.advance()?;
if close_paren.kind == TokenKind::CloseParen {
return Ok(expr);
} else {
return Err(ParseError::UnexpectedToken {
found: close_paren.kind,
span: close_paren.span,
expected: &[TokenKind::CloseParen],
});
}
},
// something unexpected
_ => {},
}
// We couldn't parse the `factor` so try to return a nice error
// indicating what types of tokens we were expecting
match self.tokens.next() {
// "we found an XXX but were expecting a number, identifier, or minus"
Some(Ok(Token { span, kind, .. })) => {
Err(ParseError::UnexpectedToken {
found: kind,
expected: &[TokenKind::Number, TokenKind::Identifier, TokenKind::Minus],
span,
})
},
// the underlying tokens stream encountered an error (e.g. unknown
// character)
Some(Err(e)) => Err(e),
// there were just no tokens available to parse as a factor
None => Err(ParseError::UnexpectedEndOfInput),
}
}
}
We are also in a better position to report parse errors here because we’ve reached several terminals (branches/rules which don’t recurse). If possible, we try to let the user know what type of token we were expecting to see.
To keep the match statement from growing out of control I’ve pulled
matching either a variable or function call (both of which start with an
identifier) out into its own function. However if you look at the rule for
parenthesised expressions you can probably figure out how it goes.
Sorry if it feels like I’ve rushed this section. I’ve written enough recursive descent parsers that it tends to be a mechanical process and once you’ve seen how to write one or two rules, you can write pretty much anything.
Testing Link to heading
Something I can’t overstate enough when writing a parser by hand is to have a reasonably large test suite with lots of edge cases.
To make the process easier I’ll often create my own macro_rules macro to
make writing tests easier.
For example, to test that we parse something correctly I’ll generate a test
that parses a string into an Expression then immediately use the
pretty-printer created earlier to turn it back into a string.
If the round-tripped version matches the original you can be fairly confident your parser is correct without having to write out verbose parse trees by hand.
// src/parse.rs
#[cfg(test)]
mod parser_tests {
use super::*;
macro_rules! parser_test {
($name:ident, $src:expr) => {
parser_test!($name, $src, $src);
};
($name:ident, $src:expr, $should_be:expr) => {
#[test]
fn $name() {
let got = Parser::new($src).parse().unwrap();
let round_tripped = got.to_string();
assert_eq!(round_tripped, $should_be);
}
};
}
}
And here are some of my parser tests:
// src/parse.rs
#[cfg(test)]
mod parser_tests {
...
parser_test!(simple_integer, "1");
parser_test!(one_plus_one, "1 + 1");
parser_test!(one_plus_one_plus_negative_one, "1 + -1");
parser_test!(one_plus_one_times_three, "1 + 1*3");
parser_test!(one_plus_one_all_times_three, "(1 + 1)*3");
parser_test!(negative_one, "-1");
parser_test!(negative_one_plus_one, "-1 + 1");
parser_test!(negative_one_plus_x, "-1 + x");
parser_test!(number_in_parens, "(1)", "1");
parser_test!(bimdas, "1*2 + 3*4/(5 - 2)*1 - 3");
parser_test!(function_call, "sin(1)");
parser_test!(function_call_with_expression, "sin(1/0)");
parser_test!(
function_calls_function_calls_function_with_variable,
"foo(bar(baz(pi)))"
);
}
The tokeniser tests are quite similar, except we also need to make sure spans are correct otherwise the user will get dodgy error messages.
// src/parse.rs
#[cfg(test)]
mod tokenizer_tests {
use super::*;
macro_rules! tokenize_test {
($name:ident, $src:expr, $should_be:expr) => {
#[test]
fn $name() {
let mut tokens = Tokens::new($src);
let got = tokens.next().unwrap().unwrap();
let Range { start, end } = got.span;
assert_eq!(start, 0);
assert_eq!(end, $src.len());
assert_eq!(got.kind, $should_be);
assert!(
tokens.next().is_none(),
"{:?} should be empty",
tokens
);
}
};
}
}
And this is what they look like in action.
// src/parse.rs
impl tokenizer_tests {
...
tokenize_test!(open_paren, "(", TokenKind::OpenParen);
tokenize_test!(close_paren, ")", TokenKind::CloseParen);
tokenize_test!(plus, "+", TokenKind::Plus);
tokenize_test!(minus, "-", TokenKind::Minus);
tokenize_test!(times, "*", TokenKind::Times);
tokenize_test!(divide, "/", TokenKind::Divide);
tokenize_test!(single_digit_integer, "3", TokenKind::Number);
tokenize_test!(multi_digit_integer, "31", TokenKind::Number);
tokenize_test!(number_with_trailing_dot, "31.", TokenKind::Number);
tokenize_test!(simple_decimal, "3.14", TokenKind::Number);
tokenize_test!(simple_identifier, "x", TokenKind::Identifier);
tokenize_test!(longer_identifier, "hello", TokenKind::Identifier);
tokenize_test!(
identifiers_can_have_underscores,
"hello_world",
TokenKind::Identifier
);
tokenize_test!(
identifiers_can_start_with_underscores,
"_hello_world",
TokenKind::Identifier
);
tokenize_test!(
identifiers_can_contain_numbers,
"var5",
TokenKind::Identifier
);
}
Conclusions Link to heading
While our main focus is implementing a geometric constraints solver, this
article mainly focused on defining our Expression tree’s structure and
converting to/from its string representation.
Now we’ve got a way to represent Expressions, enter them into a program, and
print them out for debugging, we’ve created a solid foundation that the rest of
the solver can be built on.
As an aside, the code and techniques used here are almost identical to those
used when implementing a programming language. Indeed, that’s where I
initially learned things like Backus–Naur form (the syntax used to
represent rules), Recursive Descent parsers, and
LL(1) grammars.